Riemannian preconditioning
Authors
B. Mishra and R. Sepulchre
Abstract
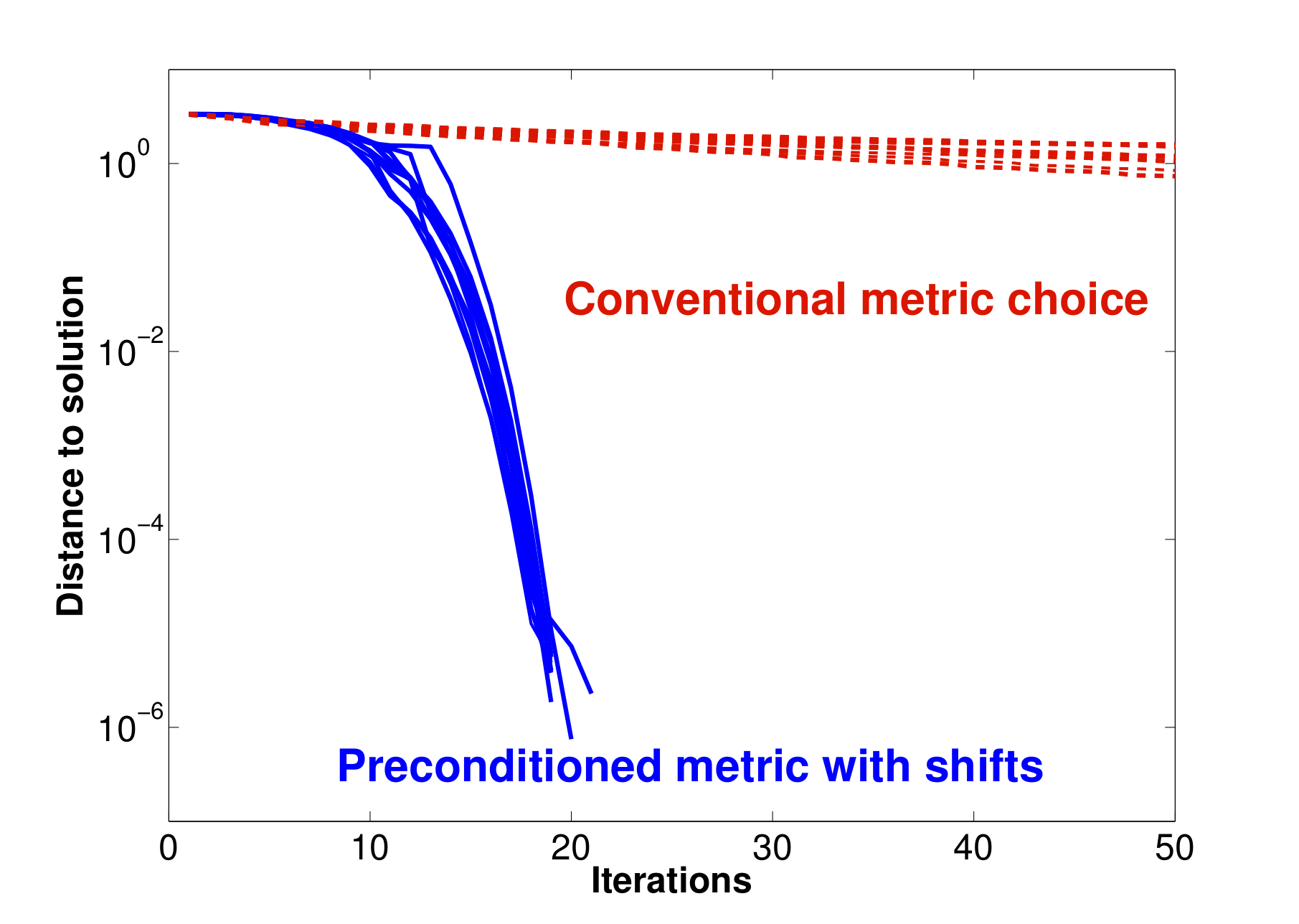
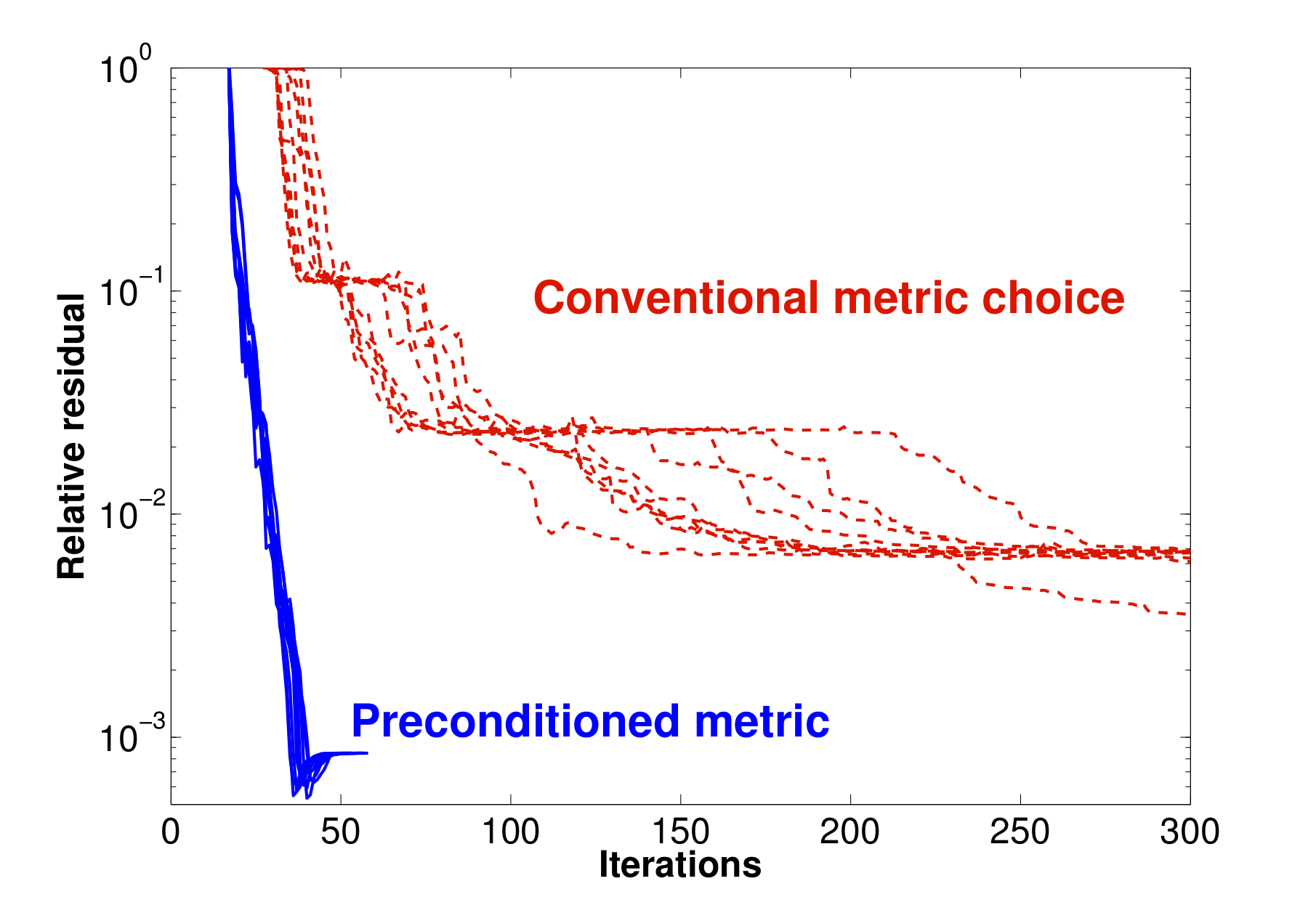
The paper exploits a basic connection between sequential quadratic programming and Riemannian gradient optimization to address the general question of selecting a metric in Riemannian optimization, in particular when the Riemannian structure is sought on a quotient manifold. The proposed method is shown to be particularly insightful and efficient in quadratic optimization with orthogonality and/or rank constraints, which covers most current applications of Riemannian optimization in matrix manifolds.
Downloads
- Status: SIAM Journal on optimization, 26(1), pp. 635 – 660, 2016.
- Paper: [arXiv:1405.6055] [Publisher’s pdf].
Examples
 |
 |
Bamdev Mishra 