A Riemannian three-factor algorithm for low-rank matrix completion
Authors
B. Mishra and R. Sepulchre
Abstract
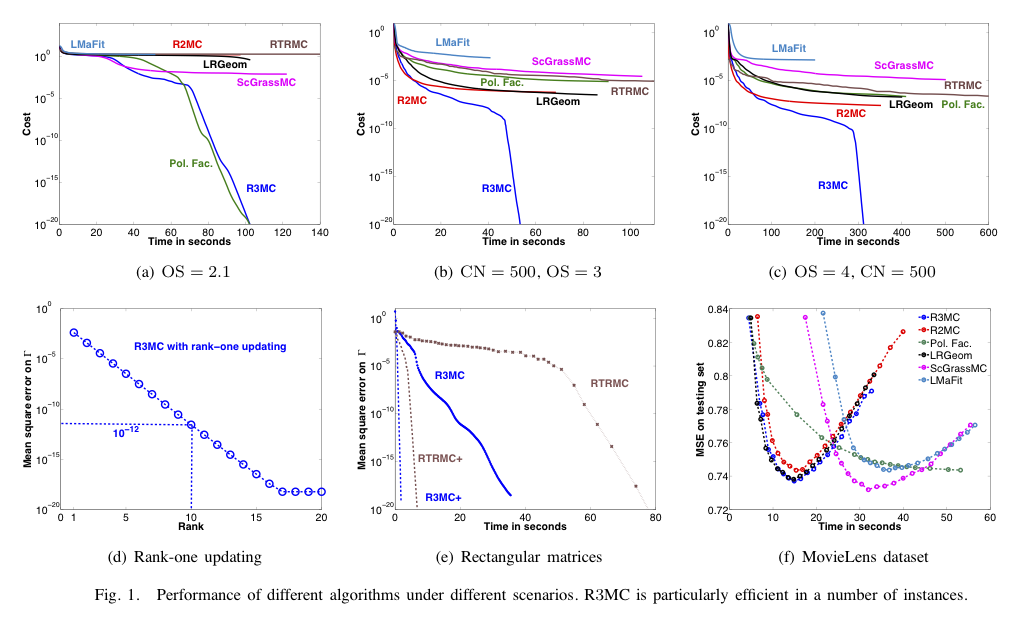
We exploit the versatile framework of Riemannian optimization on quotient manifolds to implement R3MC, a nonlinear conjugate gradient method optimized for matrix completion. The underlying geometry uses a Riemannian metric tailored to the quadratic cost. Numerical comparisons suggest that R3MC robustly outperforms state-of-the-art algorithms across different synthetic and real datasets especially in instances that combine scarcely sampled and ill-conditioned data.
Downloads
- Status: Published in the proceedings of the 53rd IEEE Conference on Decision and Control, 2014.
- Paper: [Publisher’s pdf] [arXiv:1306.2672]
- Matlab code: R3MC_30sep_2020.zip (updated on 30 sep 2020: included rank updating strategy, 17 feb 2017: excluded the time used for computing the test predictions).
- Entry: June 13, 2013: The code is online.