RPrecon tensor completion

Low-rank tensor completion: a Riemannian manifold preconditioning approach

Authors

H. Kasai and B. Mishra

Abstract

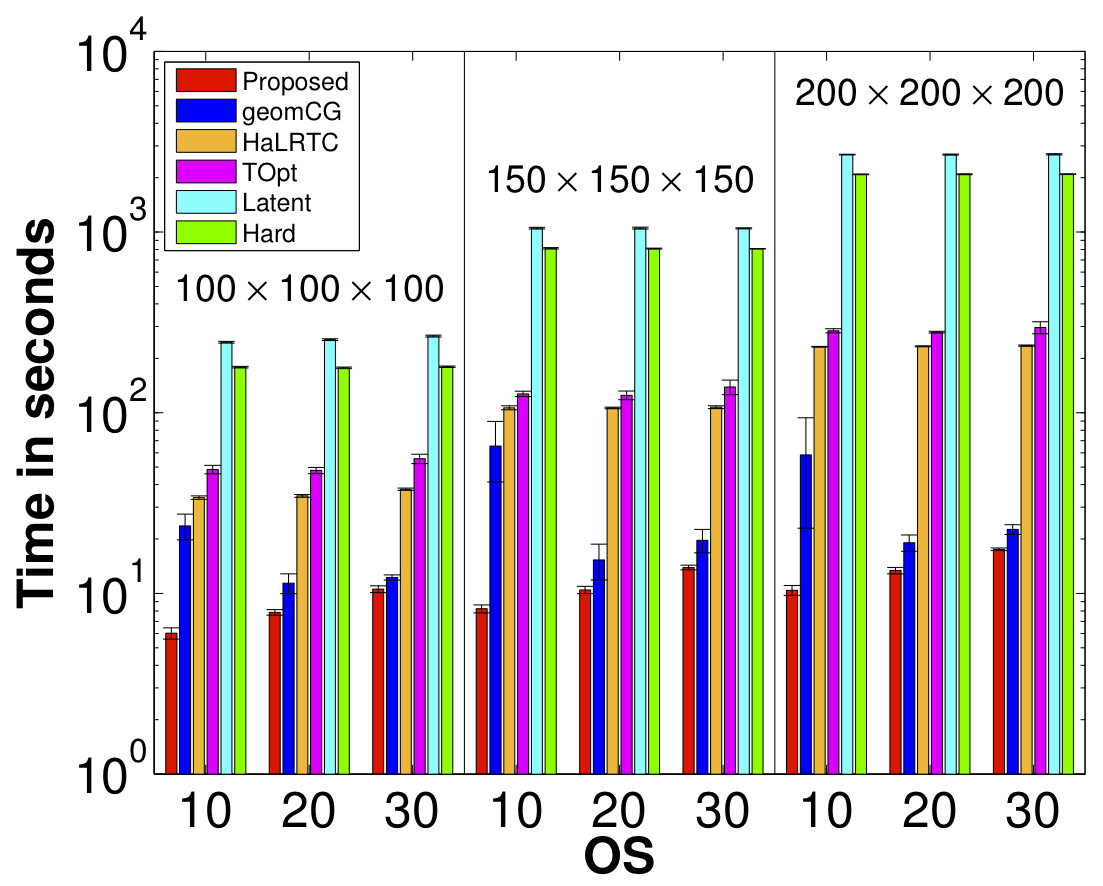
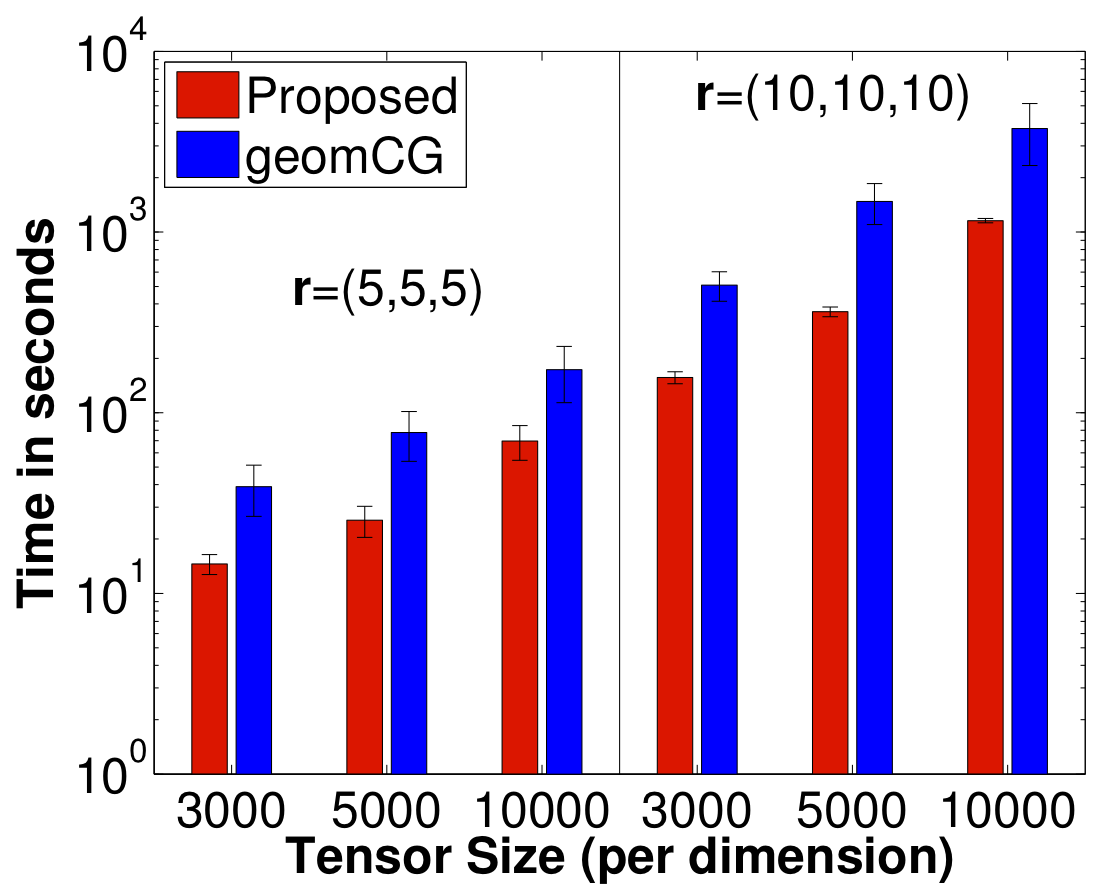
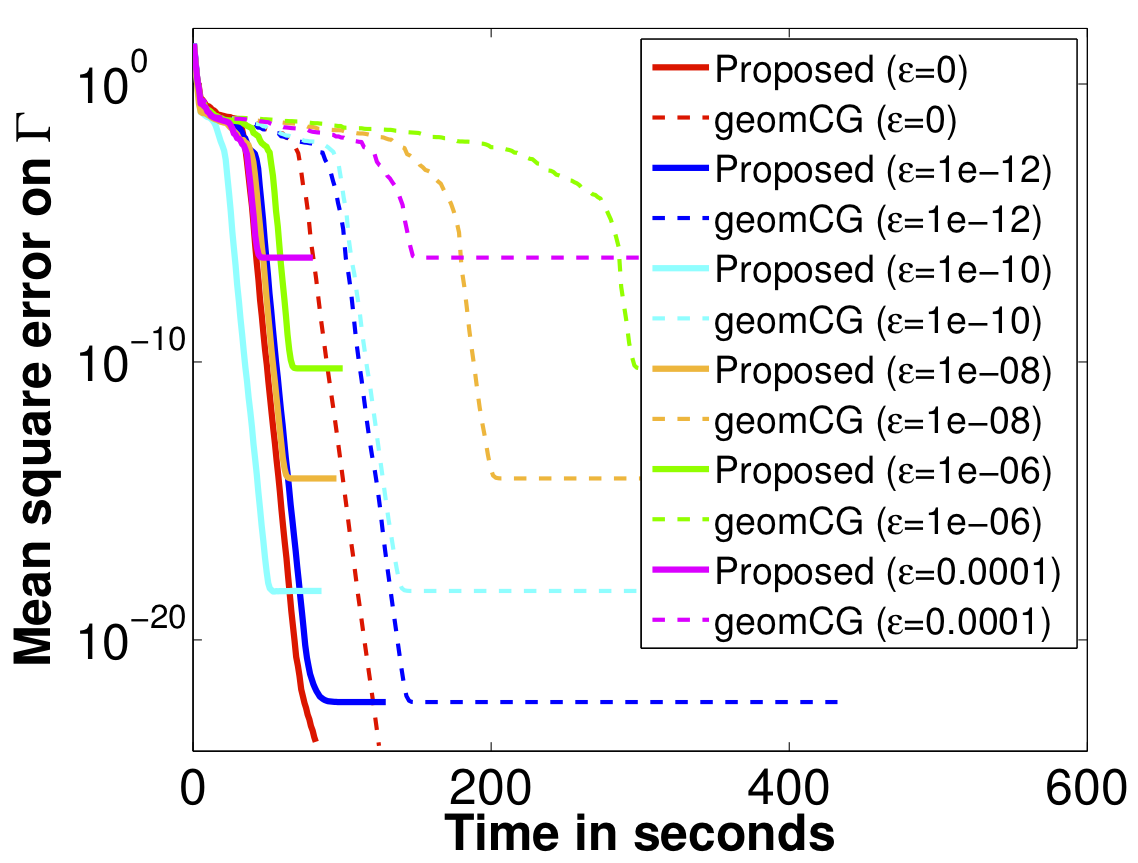
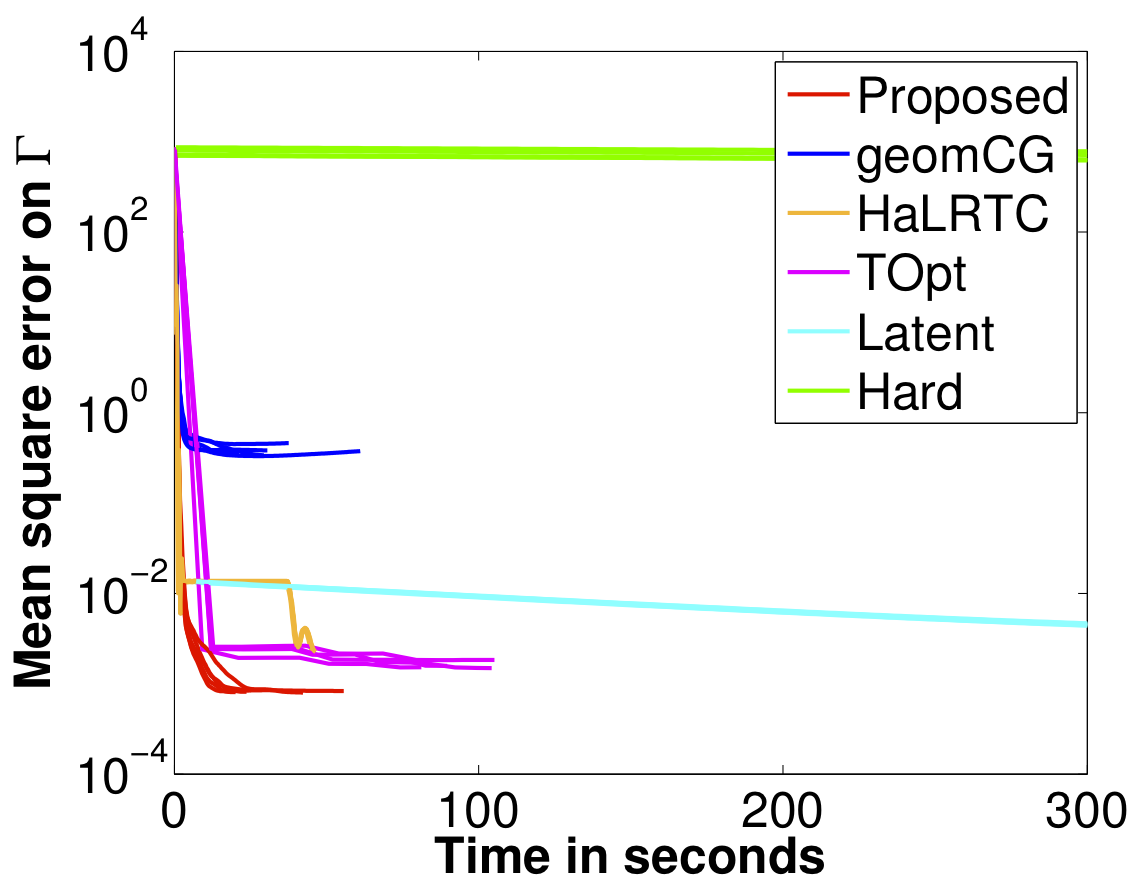
We propose a novel Riemannian manifold preconditioning approach for the tensor completion problem with rank constraint. A novel Riemannian metric or inner product is proposed that exploits the least-squares structure of the cost function and takes into account the structured symmetry that exists in Tucker decomposition. The specific metric allows to use the versatile framework of Riemannian optimization on quotient manifolds to develop preconditioned nonlinear conjugate gradient and stochastic gradient descent algorithms for batch and online setups, respectively. Concrete matrix representations of various optimization-related ingredients are listed. Numerical comparisons suggest that our proposed algorithms robustly outperform state-of-the-art algorithms across different synthetic and real-world datasets.

Downloads

• Status: ICML 2016. A shorter version was earlier accepted to 8th NeurIPS workshop on optimization for machine learning (OPT2015) held at Montreal, Canada on December 11, 2015. Extension to the general tensor learning problems is here.
• Paper: [Publisher’s copy] [Supplementary material] [arXiv:1605.08257].
  • Old version: [arXiv:1506.02159]. Since then, we have discussed an online algorithm. The title has been changed subsequently.
• GitHub codes: Here.
• Matlab code: Rprecon_for_tensor_completion_1July2016.zip
  • 01 July 2016: added functionality for regularization and weighted tensor completion.
  • Added tucker2multiarray.m file on 21 July 2015.
  • Note: The implementation is based on Manopt.
  • Entry: 09 June 2015.
• The file low_rank_tensor_completion_KM.m shows both first and second order implementations for the tensor completion problem with Manopt. It shows the Euclidean and Riemannian Hessian computations, which could be an involved task for many.
• Contribution to Manopt: we provide a Manopt factory file that allows to perform low-rank tensor optimization beyond the tensor completion problem. It can be readily called with all (including second order) of Manopt’s sovlers.
• Poster: Riemannian preconditioning for tensor completion in Low-rank Optimization and Applications workshop, Hausdorff Center for Mathematics, Bonn, 2015.

Examples