A Riemannian geometry for low-rank matrix completion
This package contains a Matlab implementation of algorithms for the low-rank matrix completion problem. The present version includes gradient descent, conjugate gradient, and trust-region algorithms based on the fixed-rank geometry proposed in the technical report [arXiv:1211.1550].
Authors
B. Mishra, K. Adithya Apuroop, and R. Sepulchre
Abstract
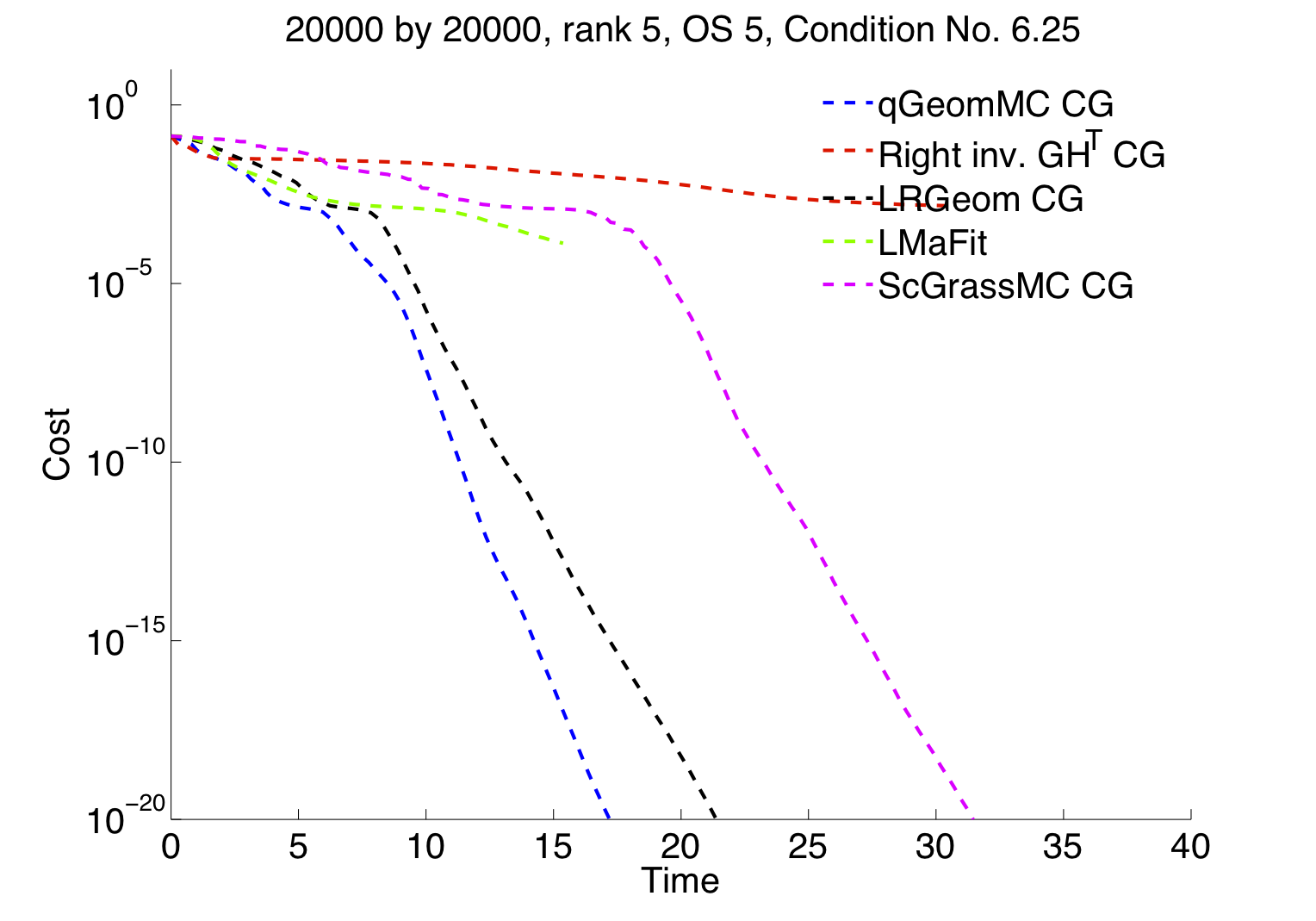
We propose a new Riemannian geometry for fixed-rank matrices that is specifically tailored to the low-rank matrix completion problem. Exploiting the degree of freedom of a quotient space, we tune the metric on our search space to the particular least square cost function. At one level, it illustrates in a novel way how to exploit the versatile framework of optimization on quotient manifold. At another level, our algorithm can be considered as an improved version of LMaFit, the state-of-the-art Gauss-Seidel algorithm. We develop necessary tools needed to perform both first-order and second-order optimization. In particular, we propose gradient descent schemes (steepest descent and conjugate gradient) and trust-region algorithms. We also show that, thanks to the simplicity of the cost function, it is numerically cheap to perform an exact linesearch given a search direction, which makes our algorithms competitive with the state-of-the-art on standard low-rank matrix completion instances.
Benchmarks
We wish to state that the following codes are the ones provided by their individual authors. Any omission if brought to notice, will be duly corrected. The package contains implementations that may not be up-to-date. Interested users are pointed to the links below.
- LRGeom: Trust-region (TR) + Conjugate Gradient (CG) + Steeepest descent (SD)
- RTRMC: TR + SD
- ScGrassMC: CG + SD
- LMaFit: Alternating minimization
- Full-rank (GH^T) in [arXiv:1209.0430]: TR + CG + SD
- SVD-like (UBV^T) factorization based on [arXiv:1112.2318]: TR + CG + SD + Accel. linearized linesearch
- Subspace-projection (UY^T) factorization in [arXiv:1209.0430]: TR + CG + SD + Accel. linearized linesearch
Downloads
- Status: Technical report
- Paper: [arXiv:1211.1550]
- Matlab code: qGeomMC_30april_2013.zip