Bamdev Mishra

Applied Machine Learning Researcher

Low-rank Riccati solutions

A Riemannian approach to low-rank algebraic Riccati equations

Authors:

B. Mishra and B. Vandereycken

Abstract

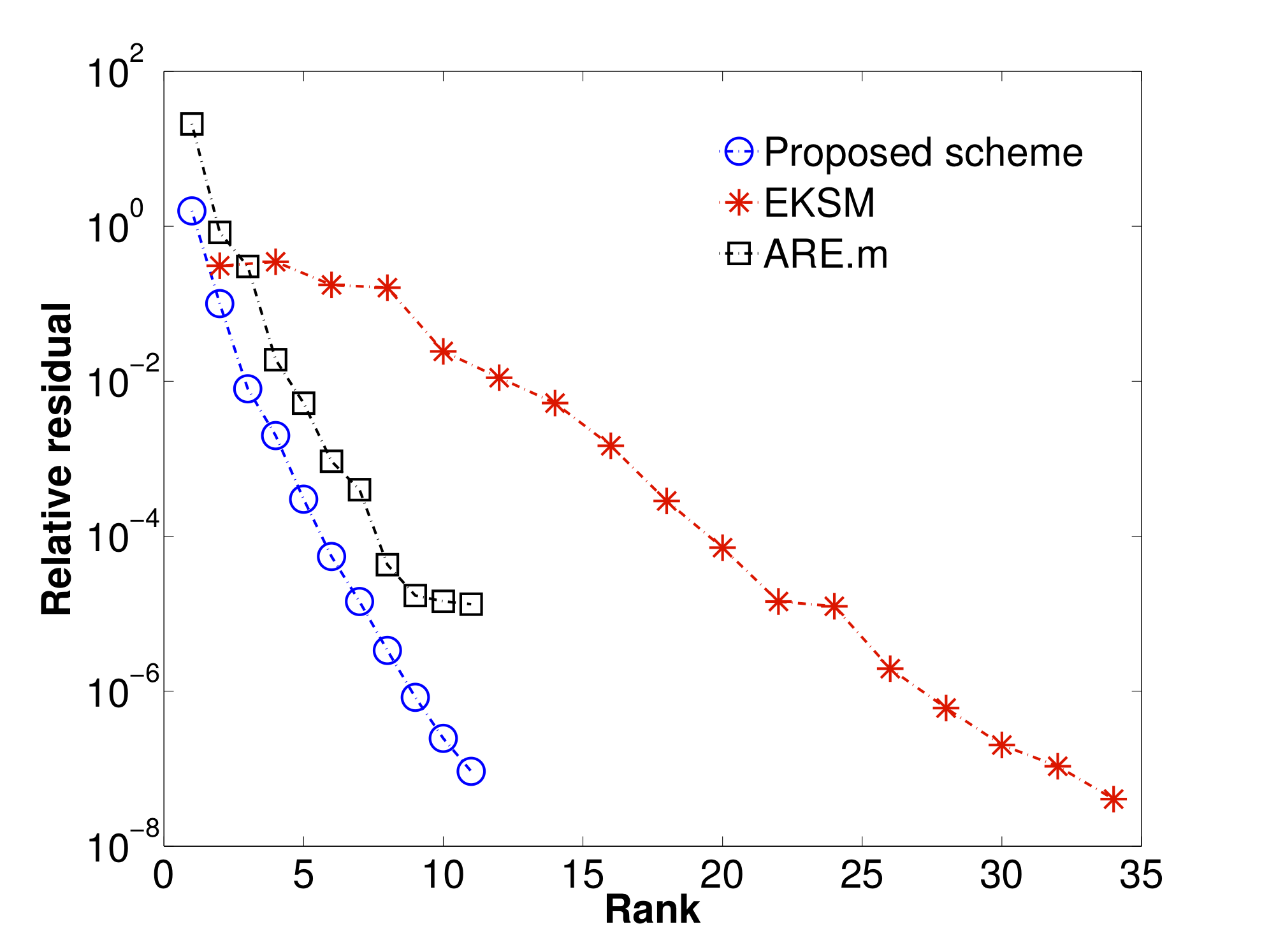
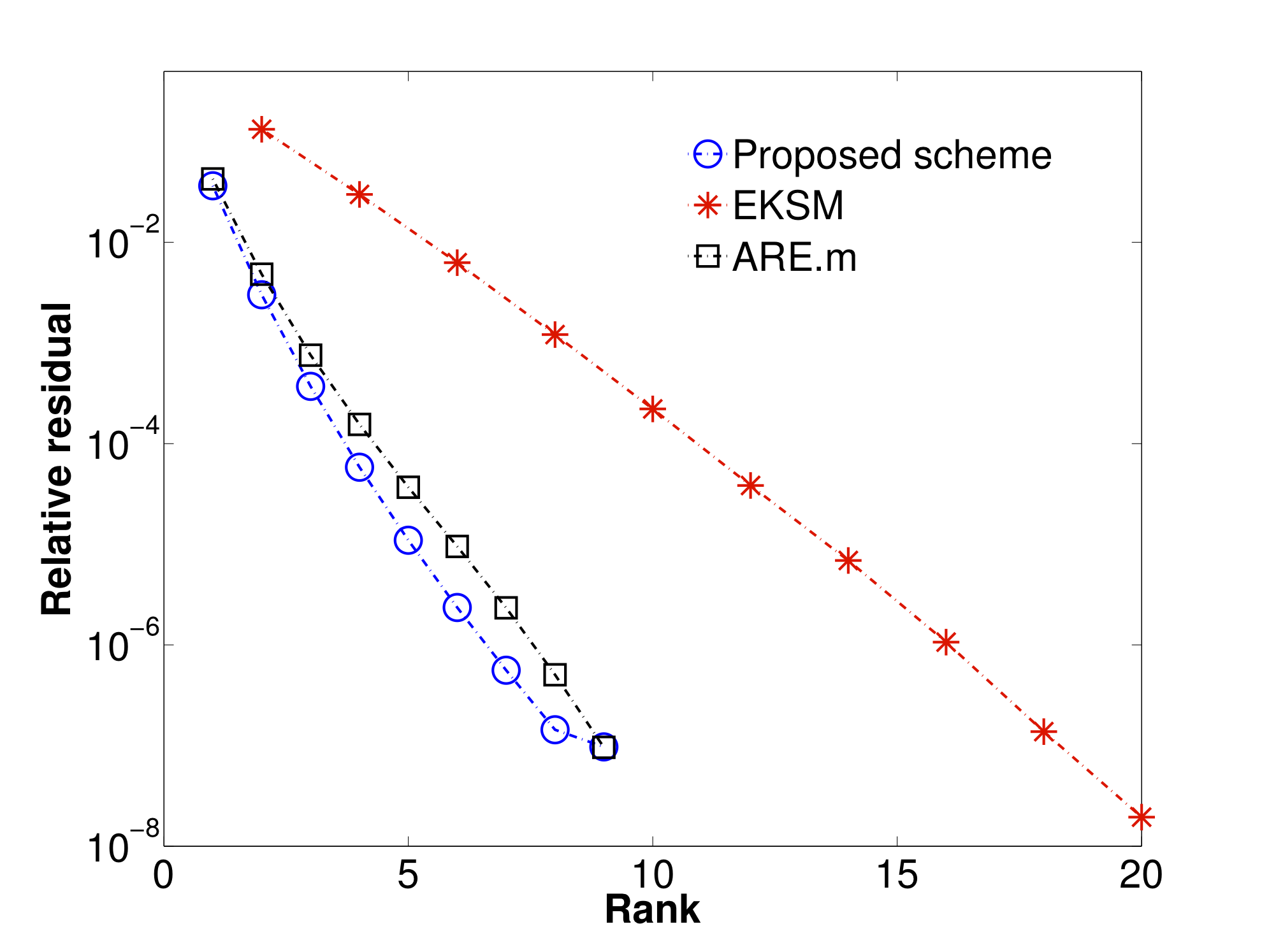
We propose a Riemannian optimization approach for computing low-rank solutions of the algebraic Riccati equation. The scheme alternates between fixed-rank optimization and rank-one updates. The fixed-rank optimization is on the set of fixed-rank symmetric positive definite matrices which is endowed with a particular Riemannian metric (and geometry) that is tuned to the structure of the objective function. We specifically discuss the implementation of a Riemannian trust-region algorithm that is potentially scalable to large-scale problems. The rank-one update is based on a descent direction that ensures a monotonic decrease of the cost function. Preliminary numerical results on standard small-scale benchmarks show that we obtain solutions to the Riccati equation at lower ranks than the standard approaches.

Downloads

Note

We solve the equation ATX + XA + X BBT X = CTC for X on the low-rank manifold of symmetric and positive definite matrices, where A is large and sparse, B is a tall matrix, and C is a fat matrix. For B = 0, this boils down to the continuous Lyapunov equation.

The code has been tuned for large-scale problems, i.e., each iteration is computationally feasible pending an efficient solver for the linear system Px = b, where P is sparsely-structured, often an outcome of the problem formulation itself. In the present code, Px = b for smaller to moderate size problems (up to 10000-by-10000 size matrices) is solved with the backslash operator of Matlab without any tuning. For larger size matrices, we employ the Matlab’s built-in iterative pcg solver without any tuning, which may not be efficient for all problems. Specific problems call for specific solvers! If you are interested in a particular setup and have a solver, then do look for the function “use_iterative_solver” in the file “Main_files/Riemannian_lowrank_riccati.m” and modify it accordingly.

The code is built on the Manopt platform. Feel free to contact me on any issue.

Examples

Discretization of one-dimensional heat equation with Dirichlet boundary.
Discretization of the Laplace operator.
%d bloggers like this: